https://gall.dcinside.com/mgallery/board/view/?id=drawing&no=60175
<투시> 원기둥을 그려보자 - 그림 갤러리
원기둥을 본격적으로 설명하기에 앞서서 일단 2점투시의 소실점을 다시한번 살펴보자90도로 꺾여있는 직육면체의 회전을 구하기 위해 90도로 꺾은 선을 SP에서 회전시킨다는게 뭔가 의미 심장하
gall.dcinside.com
원기둥을 본격적으로 설명하기에 앞서서 일단 2점투시의 소실점을 다시한번 살펴보자

90도로 꺾여있는 직육면체의 회전을 구하기 위해 90도로 꺾은 선을 SP에서 회전시킨다는게 뭔가 의미 심장하지 않은가?
여기서 뭔가 알듯말듯한 기분이 들어서 잠이 안오고 파도치는 바다를 보고 있으면 막 강약약중강약으로 치는거 같은 패턴이 있는거 같고
뭔가 법칙이 있는거 아닌가 하는 기분이 들면 당신도 훌륭한 투시빌런의 길에 접어든 것이다.

즉 SP에서 어떤 각도만큼 벌려 그은선이 수평선과 만나서 만드는 소실점은

관측자로부터 어떤 각도만큼 기울어져 그어진 평행한 선들이 무한으로 연장되었을때 만나는 점을 의미하는 것이다.
그럼 이것이 원기둥과 무슨 관계가 있는가.
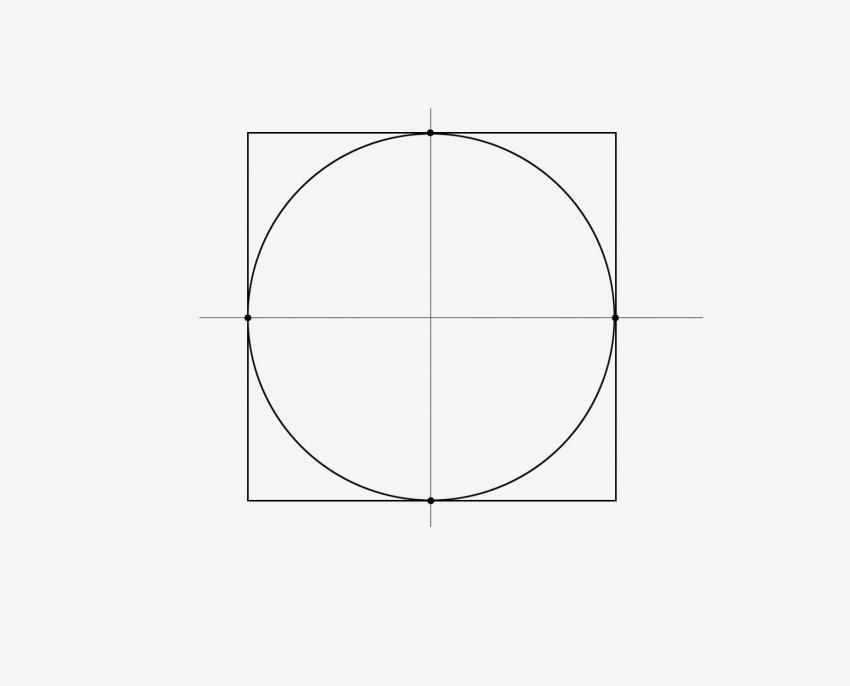
우선 원이라는게 무엇인가 한번 생각해보자. 원이라는 것이 내접하는 사각형이란 모든변의 길이가 같은 정사각형이다.

그렇다면 정사각형을 가로지르는 대각선이 이루는 각도는 몇도인가. 45도가 아니던가
그럼 여기서 바꿔말하면

SP에서 45도로 벌려서 그은선으로 만드는 소실점을 향해 그은선이 사각형을 가로지르는 대각선이라면 그 사각형은 정사각형이라는 말이 된다.
그렇다면 그 정사각형에 내접하는 타원을 그리면

그렇다. 우리는 드디어 투시상에 원을 그린 것이다.

같은 원리에 입각한 일련의 행위를 반복하면

어렵지 않게 원기둥을 그려낼수 있다.
'그림갤 > 투시' 카테고리의 다른 글
| <투시> 상자를 회전시켜보자 03 (0) | 2021.05.16 |
|---|---|
| <투시> 길을 그려보자 (0) | 2021.05.16 |
| <투시> 상자를 회전 시켜보자 02 (0) | 2021.05.16 |
| 그림쟁이를 위한 축개념을 통한 배경투시의 이해 (0) | 2021.05.16 |
| 투시 연습용 사진 (0) | 2021.05.15 |




댓글