https://m.dcinside.com/board/drawing/109164
<투시> 뭐 대각소실점이 뭐 어쩄다고? - 그림 갤러리
d[일반] 투시 고수있음 좀 도와주셈https://gall.dcinside.com/mgallery/board/view/?id=drawing&no=109125&_rk=EYz&s_type=searc
gall.dcinside.com
d[일반] 투시 고수있음 좀 도와주셈
https://gall.dcinside.com/mgallery/board/view/?id=drawing&no=109125&_rk=EYz&s_type=search_all&s_keyword=%ED%88%AC%EC%8B%9C&page=1
라는 그냥 척봐도 아무도 대답못해줄거 같이 안타까운 질문이 있길래,
또 그럴땐 친구같은 투시빌런이 등장해서 그 질문에 대한 알기쉽지는 않지만 원론적이고 근본적인 답변을 해주겠다.
혹시 SP라는걸 들어본적이 있는가? 투시빌런의 글에 항상 등장하는 마법의 점인 SP는 어째선지 내가 그 존재를 아무리 부르짖어도
모두가 귓등으로도 안듣는 거 같은 기분이고 그 존재를 부정한채로 뭔가들 해보려다가 주화입마가 오는데 뭐 그걸 구경하는 것도 꽤 재밌는 일이지만,
아무튼 이 SP라는 개념을 다시 한번 살펴보자

SP란 관측자의 눈높이에 위치하고 있는 한개의 점이다. 이게 이해의 편의를 돕기위해 "눈높이"라는 말을 사용하고 있지만 더 엄밀하게 말하자면
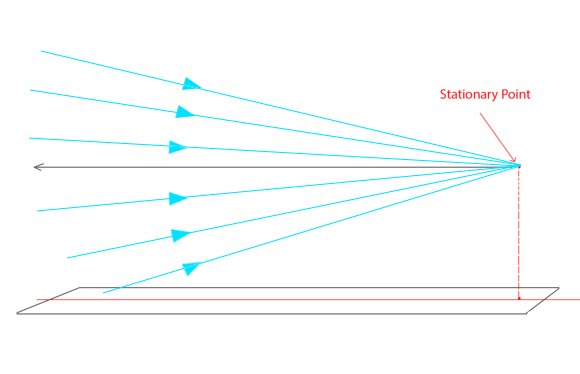
직진하고 있는 빛줄기의 다발들이 통과하는 한 점을 이야기한다.
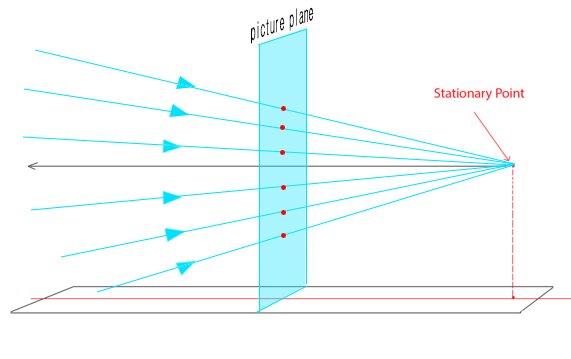
그리고 투시라는 것의 정말로 근원적인 본질은 그 선들이 픽쳐플레인에 어떻게 투영되고 있는가를 관측에 의거하여 논리적으로 풀어낸 원리 모음집 같은 것이다.
근데 여러분도 본 기억이 있겠지만 그럼
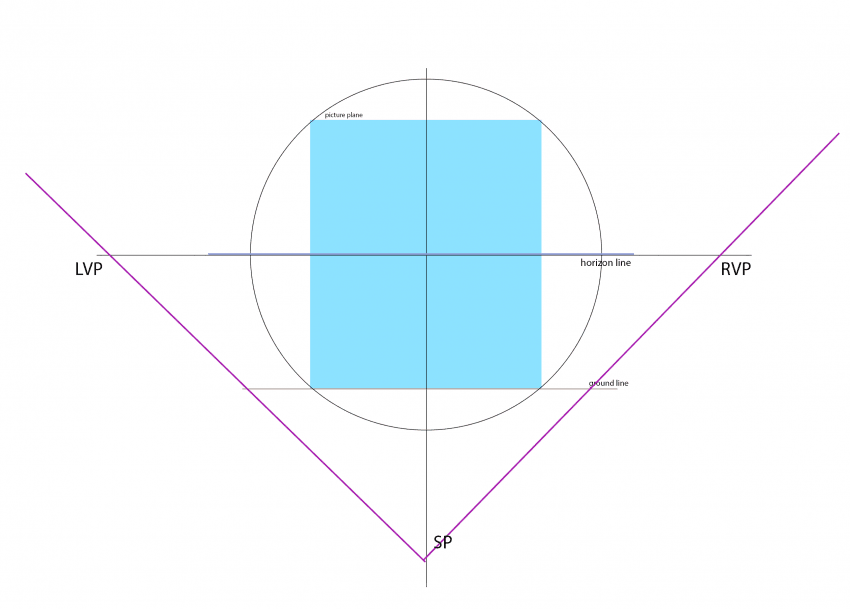
이런식으로 평면에 도식화 된 것들은 어떻게 한거냐? 아니 저거 아까 위에꺼하곤 생긴게 완전 다르잖아
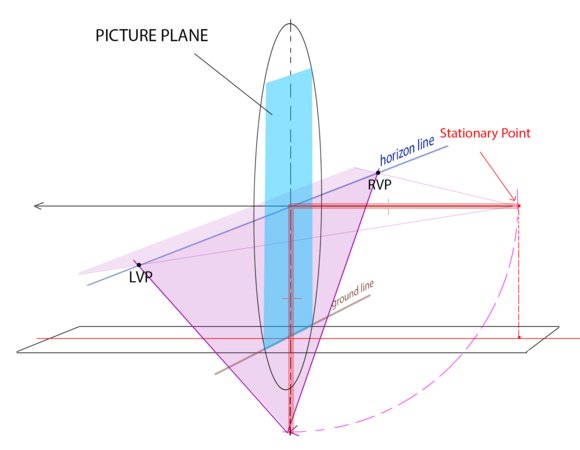
그건 픽쳐플레인과 같은 평면좌표위에 SP를 위치시켜서 계산을 용이하기 하게 위해 수직으로 한번 접어서 내린것이다.
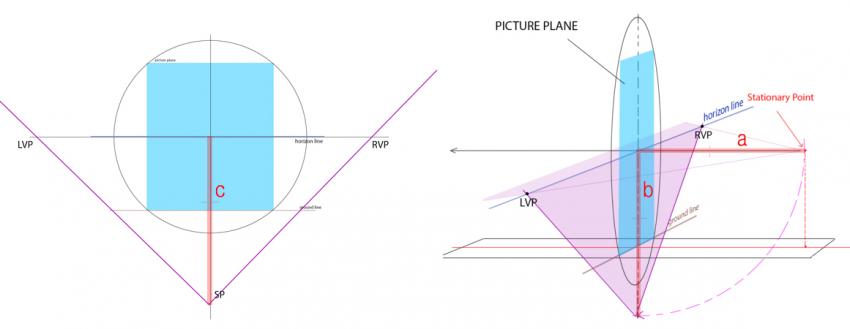
즉 SP와 픽쳐플레인으로부터의 거리인 선a의 길이와 그것을 수직으로 접어서 내린 선b의 길이, 그리고 그것을 평면에서 보고 있는 평면도의 선c의 길이는
논리적으로 따져볼때나 관측적으로 볼때나 마찬가지로 모두 같은 길이이다.
그럼 이 모든 대전제에 모두가 동의했다고 하기로 하고, 대각소실점, 즉 메져링 포인트 MP는 무엇인가
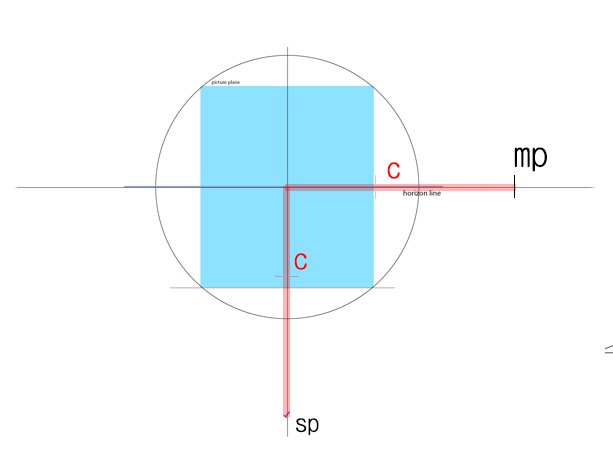
사실 "대각 소실점"같은 용어는 너무 범위가 넓은 용어라서 질문자가 본 그 자료에서 사용되기엔 좀 무리가 있는 용어이고 그 경우에는 "소실점에서 SP까지의 거리와 같은 거리만큼 소실점에서 떨어져있는 horizon line 위의 점인 MP라고 표기가 되었어야 한다. 언제나와 마찬가지로 무슨 귀신 씨나락 까먹는 소리냐 싶겠지만
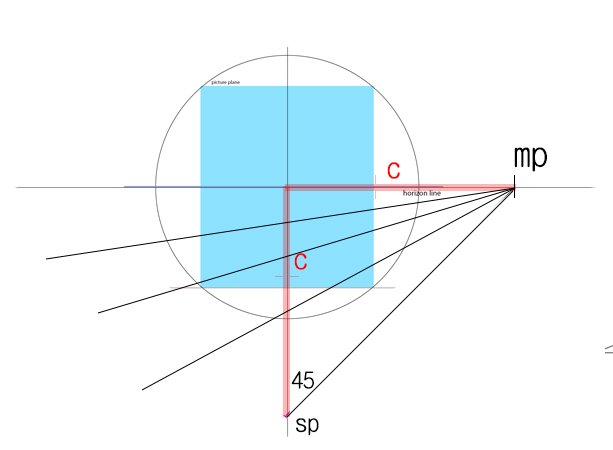
먼먼 옛날에 내가 원기둥 그리는거 설명할 때 SP로부터 45도로 그은 선과 horizon line이 만나는 곳에 찍은 점은 관측자 기준으로 45도로 그은 모든 평행선이 만나는 점이라고 했던거 기억나는가?
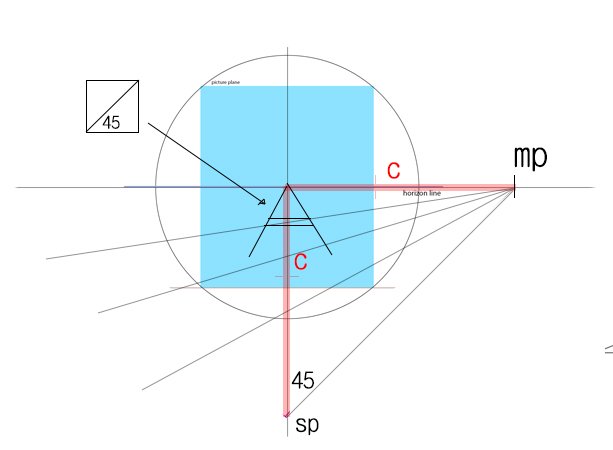
그리고 이 원리로 정사각형 찾았던건 기억 나는가? 기억 안나면 곤란하니 https://gall.dcinside.com/mgallery/board/view/?id=drawing&no=60175&_rk=urT&exception_mode=recommend&search_head=110&page=1 이거 보고 복습하자.
아무튼 그래서 이 긴긴 밑밥은 뭐때문에 이렇게 미친듯이 뿌렸는가. 여기서 가장 중요한 것은
MP가 소실점으로부터 떨어져있는 거리와 SP가 소실점으로 떨어져있는 거리가 같다는 것이다.
근데 그래서 뭐 어쨌단거냐 할거 같아서 그게 왜 그림이 그려지는 시야 넓이하고 직결이 되는지 알려주겠다.
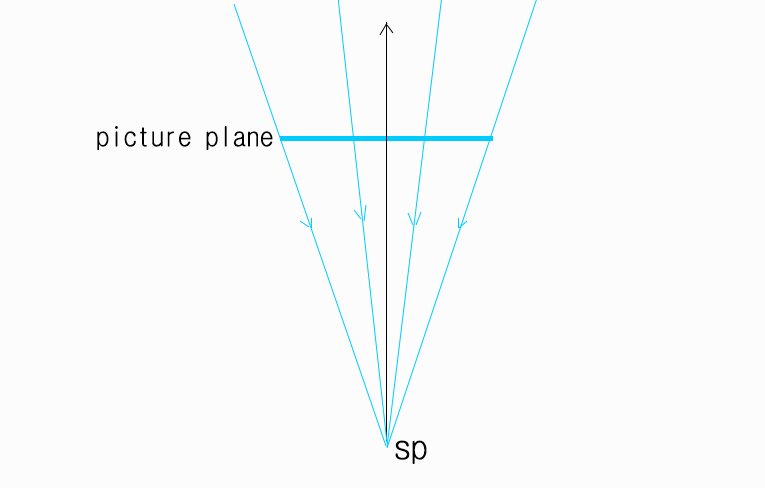
아까 위에서 "투시란 것의 본질은 SP를 통과하는 직진하는 빛의 다발들이 어떻게 픽쳐플레인에 투영되고 있는가를 다루는 것"이라고 했던것 기억나는가?
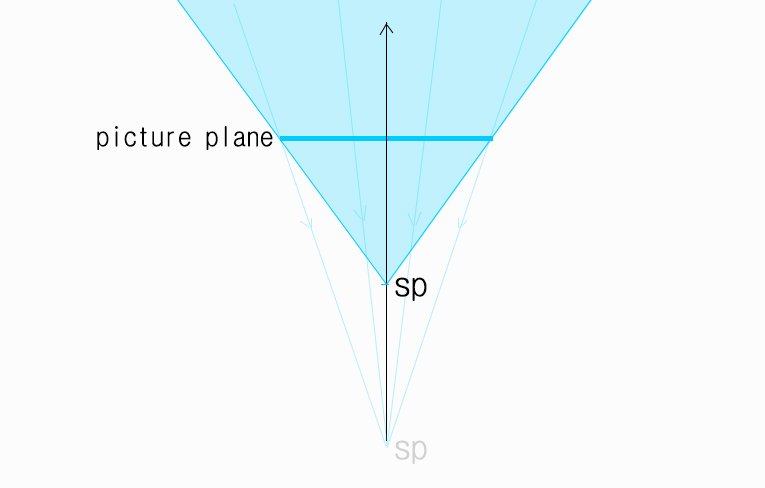
즉 같은 크기의 픽쳐플레인이 있다면 SP의 거리가 픽쳐플레인에 가까울 수록 픽쳐플레인에 투영되고 있는 상은 더 넓은 범위를 커버하게 된다는 것이다.
그렇기 때문에 위에 못든것을 종합하여, MP(대각소실점)이 소실점에 가까워지면 픽쳐플레인에 더 넓은 시야각을 그려넣게 된다는 것은 참 임을 알수 있다.
근데 이거만 보고 넘어가면 좀 아쉽잖아. 그래서 추가 내용을 준비했다.
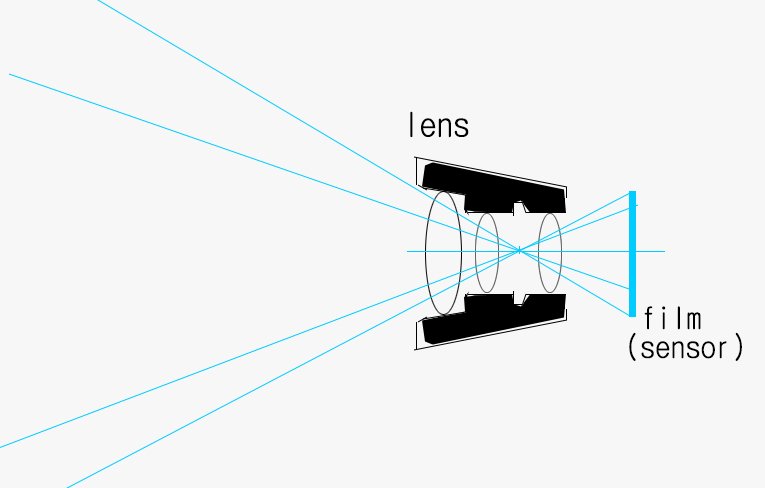
여기 뭐 대충 이렇게 생긴 렌즈하고 일정한 크기를 가진 필름 혹은 센서가 있다고 하자.
혹시 들어본적있는지 모르겠지만 렌즈에는 Focal Point라고 해서 빛이 모이는 한 지점과 여러분이 흔히 50mm 단렌즈 이런거 할때 들어봤을 Focal Length 즉 촛점 거리라는 말이 있다.
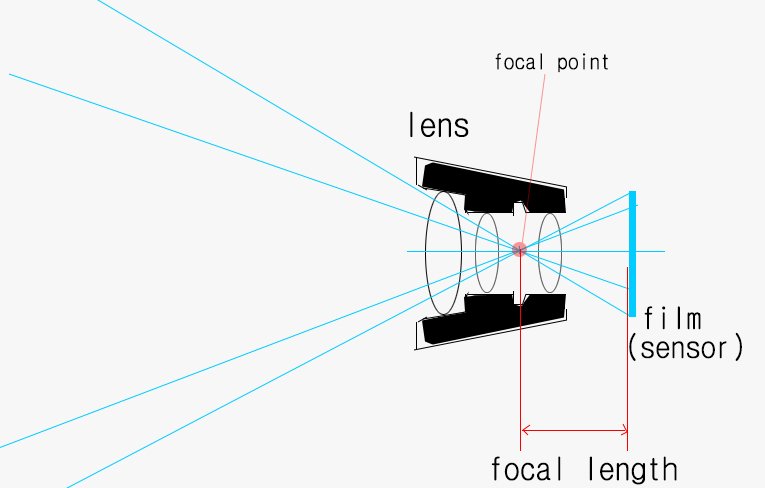
즉 흔히들 렌즈에 붙어있는 35mm니 50mm니 200mm니 하는 말은 포컬포인트가 필름이나 센서로부터 떨어져있는 거리가 35, 50, 200미리라는 뜻이다.
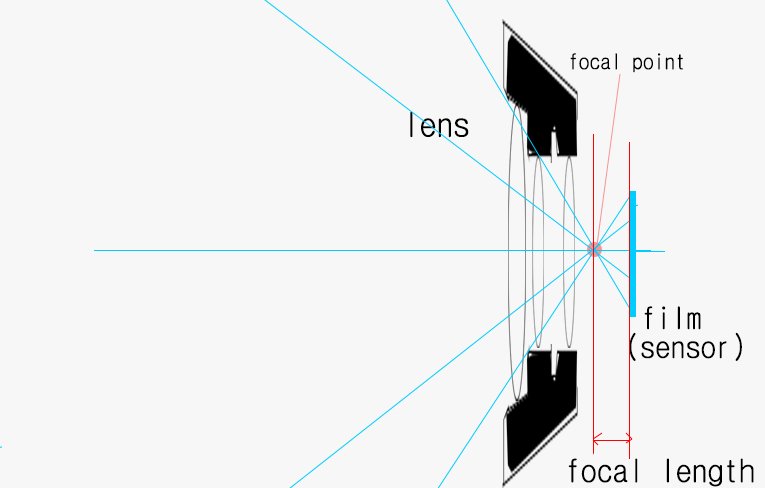
즉 렌즈의 설계를 조정하여 포컬 포인트와 정해진 사이즈의 필름이나 센서와 거리를 조정하면 이 렌즈가 얼만큼 줌렌즈인지 광각렌즈인지 조정할수 있다는 뜻이다.
괜히 무슨 12mm하면 초광각 렌즈가 200mm하면 줌렌즈인게 아니란 소리. 그렇다면 여기서 눈치빠른 사람들은 눈치를 챘겠지만 카메라 렌즈 개념도의 Focal point는 투시에서의 SP와 그 역할이 동일하며 필름이나 센서는 픽쳐플레인과 그 역할이 동일하다는 것이다. 그렇지만 왜 필름은 SP의 후면에 위치하고 픽쳐플레인은 전면에 위치해 있는데 그게 어떻게 같은거냐 할거 같은데, 그래서 필름이나 센서에 투영된 상은 뒤집혀져서 맺혀있기 때문에 우리가 보는 사진이나 영상은 그걸 한번 더 반전하는 프로세스를 거치게 된다.
...도움이 됐는지 잘 모르겠는데 하여튼 그렇다. 그럼 투시빌런 여러분 이만. 나중에 또만나요

'그림갤 > 투시' 카테고리의 다른 글
| 투시이야기 (0) | 2021.05.17 |
|---|---|
| 요시나리도 투시선 쓴다 (0) | 2021.05.17 |
| <투시빌런> 상자에 기대어 있는 기울어진 상자 (1) | 2021.05.17 |
| <투시빌런 팁 코너> 그놈의 곡면투시 (0) | 2021.05.16 |
| <투시> 평면도를 투시도로 옮겨보자 (0) | 2021.05.16 |




댓글